フーリエ級数のフーリエとは学者の名前。また級数とは数や関数の列を無限に加え合わせたものをいう。
関数がある値の倍数の周波数を持つ正弦(sin)と余弦(cos)の波、すなわち正弦波に分解されると主張する理論である。
1-2 フーリエ級数の公式
フーリエ級数の理論
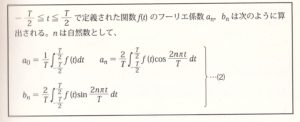
-T/2≦t≦T/2で定義された関数f(t)を考える。このf(t)が次のように正弦波の和で表せることを級数という。

※1 式(1)の形は文献によって異なる。
※定義区間は-T/2≦t≦T/2である必要はない。区間幅がTであれば、この公式は成立する
そもそも数学における級数 とは、ウィキペディアによると、ひと口に言えば数や関数など互いに足すことのできる数学的対象の列について考えられる無限項の和のことである。ただし「無限の項の総和」が何を表しているのかということはしばしば解析学の言葉を用いて様々な場合に意味を与える(級数の収束性を持つものもあれば、そのようなことができない「発散する級数」もあれば、級数自体を新たな形式的対象としてとらえることもある。小さくなっていく実数を項とする級数の収束性については様々な判定条件が与えられている。
話は元に戻って、係数a0、a1、a2、・・・an、・・・、b1、b2、・・・bn、・・・をフーリエ係数という。そして、このように関数をフーリエ級数で表すことを、その関数のフーリエ級数展開と呼ぶ。
このフーリエ級数(1)のイメージをグラフにすると以下のようになる。関数が特定の角周波数を持つ正弦波に分解できることを表している。
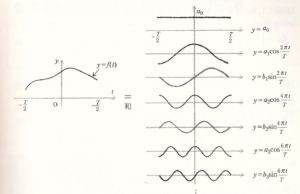
次に(1)のフーリエ係数a0、a1、a2、・・b1、b2、・・・を求める公式を示す。
フーリエ級数は時間領域から周波数領域へのマッピング
波の言葉でフーリエ級数を考える。(1)式の中の次の関数が、フーリエ級数の和を構成する基本関数系である。
1、sin2nπt/T、cos2nπt/T(nは自然数)
これらは周波数νn=n/T(角周波数ωn=2nπ/T)の正弦波である。すると、フーリエ級数(1)は関数f(t)を周波数νn(角周波数ωn)の正弦波に分解していることになる。関数f(t)がどのような周波数成分でできているかを定量的に示してくれるのである。
1-3 周期関数のときのフーリエ級
フーリエ級数は変動現象で主な分析対象にしますが、多くの変動は波の特徴を持つ。ところで、波は周期関数で表される。この周期関数をフーリエ級数で表す方法を紹介する。
前節では、区間幅Tで定義された関数f(t)を正弦波の和で表した。ところで、その正弦波を表わす三角関数は「有限」の範囲に限るものではない。そこで、この有限という範囲制限を解除したら、フーリエ級数はどんあ関数を表すか。
答えは簡単、フーリエ級数を構成する三角関数は区間幅Tだけずらしても同じ値をとる。すなわち、フーリエ級数は周期Tの周期関数を表す。
すると、フーリエ級数は周期Tの関数f(t)を表すすなわち、前節で見たフーリエ級数はTを周期とする周期関数にもそのまま適用できる。
